Difference between revisions of "MATLAB1"
| (15 intermediate revisions by the same user not shown) | |||
| Line 6: | Line 6: | ||
Rather than re-invent the wheel, we'll use some tried and tested tutorial material. The following notes from the Maths department at the University of Dundee are concise, comprehensive, but also easy to read: | Rather than re-invent the wheel, we'll use some tried and tested tutorial material. The following notes from the Maths department at the University of Dundee are concise, comprehensive, but also easy to read: | ||
http://www.maths.dundee.ac.uk/ftp/na-reports/MatlabNotes.pdf | http://www.maths.dundee.ac.uk/ftp/na-reports/MatlabNotes.pdf | ||
| + | |||
| + | Once you have read through and understood the above notes, you might like to try your hand at some example exercises: | ||
| + | * easier ones: http://www.facstaff.bucknell.edu/maneval/help211/basicexercises.html | ||
| + | * harder ones: http://www.cl.cam.ac.uk/teaching/2006/UnixTools/matlab-answers.pdf | ||
=Hints and Tips on Performance= | =Hints and Tips on Performance= | ||
| − | + | A common query is, '''"How can I speed up my MATLAB code?"'''. People often go on to say that it ran fine when they were developing their code, but now that their ambition has grown and they are working on larger problems, they end up waiting for days to get a result. This is sometimes followed up by, "it'll run faster on the HPC system, right?" Well, not necessarily. | |
| + | |||
| + | Let's try to pick some of this apart. | ||
| + | |||
| + | There are several aspects of some MATLAB code that can really limit it's performance. For loops are a common limiting factor, as is allocation of memory on-the-fly. These limitations can often be addressed by: | ||
| − | * | + | * Pre-allocation memory, where appropriate. |
| + | * Replacing loops over the elements of a vector or matrix with: | ||
** Scalar and array operations. | ** Scalar and array operations. | ||
** Built-in functions which take vectors or matrices as arguments. | ** Built-in functions which take vectors or matrices as arguments. | ||
| − | |||
| − | + | However, before we get into examples of improved code, we need to determine '''where''' your code is spending the majority of it's time. It would not be sensible to invest lots of effort in re-writing a section of your program which took only 1% of the overall runtime. Accordingly, the next section focusses on methods for finding ''hot spots'' in your code: | |
| + | |||
| + | ==Finding where your code is slow== | ||
| + | |||
| + | Possibly the simplest way to assess the performance of a sequence of MATLAB operations is to employ the timing functions '''tic''' and '''toc'''. For example: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | tic; | ||
| + | n=1500; | ||
| + | A=rand(n); | ||
| + | B=pinv(A); | ||
| + | toc | ||
| + | </source> | ||
| + | |||
| + | gives the result: | ||
<pre> | <pre> | ||
| − | + | Elapsed time is 2.163306 seconds. | |
| − | < | + | </pre> |
| + | |||
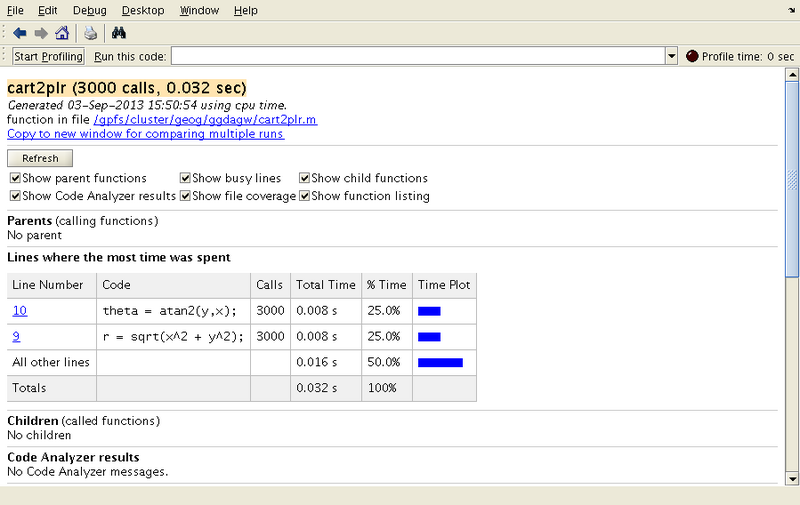
| + | A more detailed analysis can be elicited from the MATLAB profiler. Let's suppose we have a function which converts cartesian to polar coordinates: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | function [r,theta] = cart2plr(x,y) | ||
| + | % cart2plr Convert Cartesian coordinates to polar coordinates | ||
| + | % | ||
| + | % [r,theta] = cart2plr(x,y) computes r and theta with | ||
| + | % | ||
| + | % r = sqrt(x^2 + y^2); | ||
| + | % theta = atan2(y,x); | ||
| + | |||
| + | r = sqrt(x^2 + y^2); | ||
| + | theta = atan2(y,x); | ||
| + | </source> | ||
| + | |||
| + | and we call that function a number of times in the following script: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | profile on | ||
| + | for i=1:3000 | ||
| + | cart2plr(rand(),rand()); | ||
| + | end | ||
| + | profile off | ||
| + | profile viewer | ||
| + | </source> | ||
| + | |||
| + | We will be able to see the following analysis in the profile viewer window: | ||
| + | |||
| + | [[Image:MATLAB-Profiler.png|thumb|800px|none|The MATLAB profiler]] | ||
| + | |||
| + | ==Preallocation of Vectors== | ||
| + | |||
| + | Memory allocation is an expensive operation. MATLAB will allow us to assign values to an array inside a loop, where the array keeps growing to accommodate all the iterations of the loop. For example: | ||
| + | |||
| + | <source lang="matlab"> | ||
| + | for i=1:1000 | ||
| + | vec(i) = i^2; | ||
| + | end | ||
| + | </source> | ||
| + | |||
| + | However, this flexibility will come at the cost of performance, as the frequent resizing of the container ''vec'' will incur many requests for additional memory for storage. Therefore, it is wise to pre-allocate storage, if you can predict ahead of time how large the container needs to be. This is probably the simplest way in which you can speed up your MATLAB code. | ||
| + | |||
| + | To demonstrate the benefit of pre-allocation, consider the following two MATLAB scripts. | ||
| + | |||
| + | '''noprealloc.m''': | ||
| + | <source lang="matlab"> | ||
| + | tic; | ||
| + | for i=1:3000, | ||
| + | for j=1:3000, | ||
| + | x(i,j)=i+j; | ||
| + | end | ||
| + | end | ||
toc | toc | ||
| + | </source> | ||
| + | |||
| + | '''prealloc.m''': | ||
| + | <source lang="matlab"> | ||
| + | tic; | ||
| + | x=zeros(3000); | ||
| + | for i=1:3000, | ||
| + | for j=1:3000, | ||
| + | x(i,j)=i+j; | ||
| + | end | ||
| + | end | ||
| + | toc | ||
| + | </source> | ||
| + | |||
| + | When we run these two scripts (on BCp2), we see a ''significant'' difference in the runtime: | ||
| + | |||
| + | <pre> | ||
| + | >> noprealloc | ||
| + | Elapsed time is 14.317089 seconds. | ||
| + | >> prealloc | ||
| + | Elapsed time is 0.279115 seconds. | ||
</pre> | </pre> | ||
| − | |||
| − | |||
==Scalar and Array Operators== | ==Scalar and Array Operators== | ||
| Line 31: | Line 125: | ||
Replace: | Replace: | ||
| − | < | + | <source lang="matlab"> |
for i = 1:length(vec) | for i = 1:length(vec) | ||
vec(i) = vec(i) * 3; | vec(i) = vec(i) * 3; | ||
end | end | ||
| − | </ | + | </source> |
with: | with: | ||
| − | < | + | <source lang="matlab"> |
vec = vec*3 | vec = vec*3 | ||
| − | </ | + | </source> |
Similarly, if you have two vectors or matrices '''of the same size''', you can perform element-by-element operations using, e.g. | Similarly, if you have two vectors or matrices '''of the same size''', you can perform element-by-element operations using, e.g. | ||
| − | < | + | <source lang="matlab"> |
m3 = m1 - m2 | m3 = m1 - m2 | ||
| − | </ | + | </source> |
Note that array versions of the multiplication, division and exponentiation operators are '''.*''', '''./''' and '''.^''', respectively. | Note that array versions of the multiplication, division and exponentiation operators are '''.*''', '''./''' and '''.^''', respectively. | ||
| Line 54: | Line 148: | ||
==Built-in Functions== | ==Built-in Functions== | ||
| − | == | + | MATLAB contains a number of built-in functions which can save you from writing a loop. Examples include: |
| + | |||
| + | * '''sum''' and '''prod''': which compute the sum or product, respectively, of all the elements of vector. | ||
| + | * '''cumsum''' and '''cumprod''': both return a vector and are the cumulative counterparts of ''''sum''' and '''prod'''. | ||
| + | * '''min''' and '''max'''. | ||
| + | * '''any''' and '''all''': will return true if any or all of the elements of a vector or matrix are true (>0), respectively. | ||
| + | * '''find''': returns the indices of a vector that satisfy the given expression. For example, '''find(vec > 7)''' returns the indices of all elements of vec that are greater than 7. | ||
| + | |||
| + | ==MEX Files== | ||
| − | + | Another route to higher performance is to outsource an identified bottleneck in you MATLAB code to a piece of compiled code written in C/C++ or Fortran. This is the MEX file approach. A good introduction to creating MEX files is: | |
| − | |||
| − | |||
| − | + | * http://classes.soe.ucsc.edu/ee264/Fall11/cmex.pdf | |
<!-- | <!-- | ||
Latest revision as of 12:08, 7 March 2014
An Introduction MATLAB
Introduction
Rather than re-invent the wheel, we'll use some tried and tested tutorial material. The following notes from the Maths department at the University of Dundee are concise, comprehensive, but also easy to read: http://www.maths.dundee.ac.uk/ftp/na-reports/MatlabNotes.pdf
Once you have read through and understood the above notes, you might like to try your hand at some example exercises:
- easier ones: http://www.facstaff.bucknell.edu/maneval/help211/basicexercises.html
- harder ones: http://www.cl.cam.ac.uk/teaching/2006/UnixTools/matlab-answers.pdf
Hints and Tips on Performance
A common query is, "How can I speed up my MATLAB code?". People often go on to say that it ran fine when they were developing their code, but now that their ambition has grown and they are working on larger problems, they end up waiting for days to get a result. This is sometimes followed up by, "it'll run faster on the HPC system, right?" Well, not necessarily.
Let's try to pick some of this apart.
There are several aspects of some MATLAB code that can really limit it's performance. For loops are a common limiting factor, as is allocation of memory on-the-fly. These limitations can often be addressed by:
- Pre-allocation memory, where appropriate.
- Replacing loops over the elements of a vector or matrix with:
- Scalar and array operations.
- Built-in functions which take vectors or matrices as arguments.
However, before we get into examples of improved code, we need to determine where your code is spending the majority of it's time. It would not be sensible to invest lots of effort in re-writing a section of your program which took only 1% of the overall runtime. Accordingly, the next section focusses on methods for finding hot spots in your code:
Finding where your code is slow
Possibly the simplest way to assess the performance of a sequence of MATLAB operations is to employ the timing functions tic and toc. For example:
tic;
n=1500;
A=rand(n);
B=pinv(A);
toc
gives the result:
Elapsed time is 2.163306 seconds.
A more detailed analysis can be elicited from the MATLAB profiler. Let's suppose we have a function which converts cartesian to polar coordinates:
function [r,theta] = cart2plr(x,y)
% cart2plr Convert Cartesian coordinates to polar coordinates
%
% [r,theta] = cart2plr(x,y) computes r and theta with
%
% r = sqrt(x^2 + y^2);
% theta = atan2(y,x);
r = sqrt(x^2 + y^2);
theta = atan2(y,x);
and we call that function a number of times in the following script:
profile on
for i=1:3000
cart2plr(rand(),rand());
end
profile off
profile viewer
We will be able to see the following analysis in the profile viewer window:
Preallocation of Vectors
Memory allocation is an expensive operation. MATLAB will allow us to assign values to an array inside a loop, where the array keeps growing to accommodate all the iterations of the loop. For example:
for i=1:1000
vec(i) = i^2;
end
However, this flexibility will come at the cost of performance, as the frequent resizing of the container vec will incur many requests for additional memory for storage. Therefore, it is wise to pre-allocate storage, if you can predict ahead of time how large the container needs to be. This is probably the simplest way in which you can speed up your MATLAB code.
To demonstrate the benefit of pre-allocation, consider the following two MATLAB scripts.
noprealloc.m:
tic;
for i=1:3000,
for j=1:3000,
x(i,j)=i+j;
end
end
toc
prealloc.m:
tic;
x=zeros(3000);
for i=1:3000,
for j=1:3000,
x(i,j)=i+j;
end
end
toc
When we run these two scripts (on BCp2), we see a significant difference in the runtime:
>> noprealloc Elapsed time is 14.317089 seconds. >> prealloc Elapsed time is 0.279115 seconds.
Scalar and Array Operators
For example, if you would like to perform a scalar operation to a vector, vec, (say, multiply each element by 3) then you do not need to write a loop.
Replace:
for i = 1:length(vec)
vec(i) = vec(i) * 3;
end
with:
vec = vec*3
Similarly, if you have two vectors or matrices of the same size, you can perform element-by-element operations using, e.g.
m3 = m1 - m2
Note that array versions of the multiplication, division and exponentiation operators are .*, ./ and .^, respectively.
If you wish to apply the same function to all the elements of an array or vector, then you can pass it as an argument to the function. If you write your own functions, ensure that the operators that you use inside the function can handle vectors or matrices.
Built-in Functions
MATLAB contains a number of built-in functions which can save you from writing a loop. Examples include:
- sum and prod: which compute the sum or product, respectively, of all the elements of vector.
- cumsum and cumprod: both return a vector and are the cumulative counterparts of 'sum and prod.
- min and max.
- any and all: will return true if any or all of the elements of a vector or matrix are true (>0), respectively.
- find: returns the indices of a vector that satisfy the given expression. For example, find(vec > 7) returns the indices of all elements of vec that are greater than 7.
MEX Files
Another route to higher performance is to outsource an identified bottleneck in you MATLAB code to a piece of compiled code written in C/C++ or Fortran. This is the MEX file approach. A good introduction to creating MEX files is: