LinAlgebraPacks
Packages for Linear Algebra: Solving your system of equations using (optimised, bug-free) code that someone else has already written!
Introduction
This tutorial walks through a number of example programs which solve equations using linear algebra packages. These packages include LAPACK, PETSc, PLASMA and MAGMA. The examples are based upon solutions of partial differential equations (PDEs) using the Finite Difference Method (FDM). The theory of the FDM is described on NumMethodsPDEs.
The take-home message for this page is that we--as modellers and natural scientists--should be writing code at and above the level of call to a routine from a linear algebra library and we should not write code lower than this level. Why not? Well, our code will be slower (less optimised) and more likely to contain bugs. We will have wasted our time when we could have been focussing on the higher-level task of doing the science.
To download the source code for the examples, type:
svn co https://svn.ggy.bris.ac.uk/subversion-open/num-methods1 ./num-methods1LAPACK:direct solutions for dense matrices
LAPACK (which stands for Linear Algebra PACKage), is the oldest of the packages considered on this page. It has a venerable history and is still highly relevant for some problems today. The project website--which contains download instructions and a great deal of useful documentation--is: http://www.netlib.org/lapack. LAPACK is built on top of the Basic Linear Algebra Subprograms (BLAS) (http://www.netlib.org/blas), but provides a higher level functionality.
Before looking at our first example, we'll start building a 'reference' implementation of LAPACK, as it will take several minutes. First change directory to the location of the LAPACK source code that has been bundled into the repository of examples:
cd num-methods1/lapack-3.3.1
and build the libraries, by typing:
make lib
While the libraries are building, consider the following system of linear equations:
- [math]\displaystyle{ \begin{alignat}{7} x &&\; + \;&& 3y &&\; - \;&& 2z &&\; = \;&& 5 & \\ 3x &&\; + \;&& 5y &&\; + \;&& 6z &&\; = \;&& 7 & \\ 2x &&\; + \;&& 4y &&\; + \;&& 3z &&\; = \;&& 8 & \end{alignat} }[/math]
(From http://en.wikipedia.org/wiki/System_of_linear_equations.)
which we can write in matrix form:
- [math]\displaystyle{ \begin{bmatrix}1 & 3 & -2\\3 & 5 & 6\\2 & 4 & 3\end{bmatrix} \begin{bmatrix}x\\y\\z\end{bmatrix} = \begin{bmatrix}5\\7\\8\end{bmatrix} }[/math]
The following computation shows Gauss-Jordan elimination applied a further simplified (assumed the x, y and z) matrix version (Ax=b) of the above system:
- [math]\displaystyle{ \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & -4 & 12 & -8 \\ 2 & 4 & 3 & 8 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & -4 & 12 & -8 \\ 0 & -2 & 7 & -2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 & -2 & 7 & -2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & -3 & 2 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & -2 & 5 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 3 & 0 & 9 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right] }[/math][math]\displaystyle{ \sim \left[\begin{array}{rrr|r} 1 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \end{array}\right]. }[/math]
where the operations include:
- top row x3, subtract from 2nd row
- top row x2, subtract from 3rd row
etc.
OK, so far so good? Let's try our first code example:
cd ~/num-methods1/examples/example1
To see how to solve the above matrix example using LAPACK, look inside dgesv-example.f90. First the declarations:
integer, parameter :: N = 3
integer, parameter :: LDA = N ! leading dimension of A
integer, parameter :: LDB = N ! leading dimension of B
integer, parameter :: NRHS = 1 ! no. of RHS, i.e columns in b
integer, dimension(N) :: IPIV
integer :: INFO
integer :: i
real(kind=8), dimension(LDA,N) :: A ! LDAxN matrix
real(kind=8), dimension(LDB,NRHS) :: B ! LDBxNRHS matrix
Where, we see that the leading dimension of a matrix is used to specify the number of rows of storage. Note also, that we could simultaneously solve for multiple vectors B, by specifying NRHS > 1.
Next, we set up the matrix A:
! ( 1 3 -2)
! ( 3 5 6)
! ( 2 4 3)
A(1,1) = 1.0d+0
A(1,2) = 3.0d+0
A(1,3) = -2.0d+0
A(2,1) = 3.0d+0
A(2,2) = 5.0d+0
A(2,3) = 6.0d+0
A(3,1) = 2.0d+0
A(3,2) = 4.0d+0
A(3,3) = 3.0d+0
And the vector B:
! ( 5)
! ( 7)
! ( 8)
B(1,1) = 5.0d+0
B(2,1) = 7.0d+0
B(3,1) = 8.0d+0
Once we have all that in place, all we need to do is call the solver routine:
call dgesv(N, NRHS, A, LDA, IPIV, B, LDB, INFO)
Note that the solution vector replaces the values in B. (The contents of A will be changed in place too, but more of that later.)
! Print the result vector X.
! It should be:
! (-15)
! ( 8)
! ( 2)
do ii=1,LDB
write(*,*) B(ii,1)
end do
Run the program to satisfy yourself that it works:
cd num-methods1/examples/example1 make ./dgesv-example.exe
Solving Eliptical Problems using LAPACK
Next, take a look at simple-laplace.f90. This program solves the 2D laplace equation for a 4x4 domain, as described on NumMethodsPDEs. This program only differs from the previous one in way in which we initialise the matrix A and vector b. To run the program type:
./simple-laplace-expert.exe
mxm-laplace.f90 also solves our laplacian example, except that this time we can vary the size of the matrix and corresponding arrays for an mxm square domain:
./mxm-laplace.exe
LAPACK also gives us access to a routine--dgesvx--which solves the same system of equations, but also gives us some error analysis. The x stands for expert.
./mxm-laplace.exe
Exercises
- Play around with mxm-laplace.f90. Try different domain sizes, and different boundary conditions.
Details of the LU Decomposition
In practice, the LAPACK routine dgesv does not perform Gaussian elimination, but rather computes an LU decomposition and then solves the equation using two substitution steps--one forward and one backward. This is because for the same computational cost, we can factor A without knowing about b. We can then find x cheaply, for many different b. This is useful when solving parabolic equations, where x at time-step [math]\displaystyle{ j }[/math] forms the basis for b at time-step [math]\displaystyle{ j+1 }[/math].
OK, how to we obtain an LU decomposition?
The Guassian elimination process above can be expressed as a matrix multiplication. The elimination in the first column can be achieved by left multiplying A with a unit (1's on the diagonal) lower triangular matrix, [math]\displaystyle{ L_1 }[/math], with non-zeros only in the first column (this case is called an atomic unit lower triangular matrix), such as that schematically shown below:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ x & 1 & 0 \\ y & 0 & 1 \end{bmatrix} }[/math]
Following our example, [math]\displaystyle{ L_1 A=A' }[/math] becomes:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & -2 & 7 \end{bmatrix} }[/math]
The eliminations in the second column are achieved by left multiplying [math]\displaystyle{ A'=L_1 A }[/math] by [math]\displaystyle{ L_2 }[/math] (which is atomic unit lower triangular with non-zeros only in the second column):
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & -\frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ -3 & 1 & 0 \\ -2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
We note that the result [math]\displaystyle{ L_2 L_1 A = A'' = U }[/math] is upper triangular. Rearranging we get, [math]\displaystyle{ A=L_1^{-1} \cdots L^{-1}_{n-2} L^{-1}_{n-1} U }[/math]. The inverse matrices, [math]\displaystyle{ L^{-1} }[/math], are very easy to find as the inverse of an atomic unit lower triangular matrix is the same as the original save only for a change of sign in the off diagonal elements. The product is, again, unit lower triangular. Thus [math]\displaystyle{ A=LU }[/math]:
- [math]\displaystyle{ \begin{bmatrix} 1 & 3 & -2 \\ 3 & 5 & 6 \\ 2 & 4 & 3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
Given L and U we can solve Ax=b by first solving Ly=b, where:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ 3 & 1 & 0 \\ 2 & \frac{1}{2} & 1 \end{bmatrix} \begin{bmatrix}y_1\\y_2\\y_3\end{bmatrix} = \begin{bmatrix}5\\7\\8\end{bmatrix} }[/math]
As L is unit lower triangular, we can do this by easily by forward substitution:
- [math]\displaystyle{ \begin{array}{rcl} y_1 & = & 5 \\ 3 \times y_1 + y_2 & = & 7 \\ y_2 & = & 7 - 15 \\ y_2 & = & -8 \\ 10 - 4 + y_3 & = & 8 \\ y_3 & = & 12 - 10 \\ y_3 & = & 2 \end{array} }[/math]
Once we know y, we can solve Ux=y:
- [math]\displaystyle{ \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix} = \begin{bmatrix}5\\-8\\2\end{bmatrix} }[/math]
This time easily by backward substitution:
- [math]\displaystyle{ \begin{array}{rcl} x_3 & = & 2 \\ 24 - 4 \times x_2 & = & -8 \\ 32 & = & 4x_2 \\ x_2 & = & 8 \\ -4 + 24 + x_1 & = & 5 \\ x_1 & = & 9 - 24 \\ x_1 & = & -15 \end{array} }[/math]
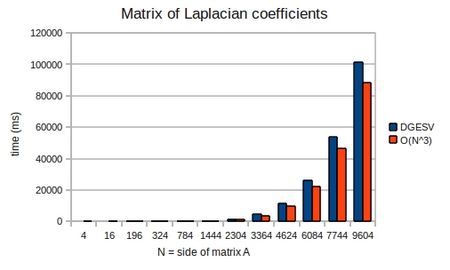
Computing the LU decomposition of an [math]\displaystyle{ n \times n }[/math] system of equations has a computational cost of [math]\displaystyle{ O(n^3) }[/math] operations, whereas the forward and backward substitution steps have a cost of [math]\displaystyle{ O(n^2) }[/math] operations. Thus the cost of solution is dominated by the LU decomposition.
To demonstrate that the solution does indeed take [math]\displaystyle{ O(n^3) }[/math] operations, I ran mxm-laplacian.exe on my desktop PC for varying sizes of N and could plot the following from the results:
If we look once again at dgesv-example.f90 and set:
logical, parameter :: verbose=.true.
(and recompile and run) we can see the contents of A after the call to dgesv(). It now contains an encoding of the LU decomposition (the unit leading diagonal from L is assumed):
LU decomposition as encoded in matrix A:
3.00000000000000 5.00000000000000 6.00000000000000
0.333333333333333 1.33333333333333 -4.00000000000000
0.666666666666667 0.500000000000000 1.00000000000000
..and the IPIV vector:
2 2 3
This is all well and good, but hang-on a cotton pickin' minute!, the matrix U is not as we expected:
- [math]\displaystyle{ \begin{bmatrix} 3 & 5 & 6 \\ 0 & \frac{4}{3} & -4 \\ 0 & 0 & 1 \end{bmatrix} \neq \begin{bmatrix} 1 & 3 & -2 \\ 0 & -4 & 12 \\ 0 & 0 & 1 \end{bmatrix} }[/math]
Why not? The answer lies the in contents of the IPIV. The elements along the leading diagonal are known as pivots. If any pivots are small, our algorithm will become unstable. We may exchange rows (known as partial pivoting) in A without changing the solution. We can read the elements of IPIV as a set of instructions for manipulating each row of the original matrix.
For example, if the first element of IPIV is a 1, then we read this as:
- exchange row 1 with row 1 (i.e. no change--a null operation)
but if the first element of IPIV were a 2, then this means:
- exchange row 1 with row 2 (i.e. swap round the firs two rows)
In the case of our example program, the following sequence of actions were performed:
- row 1 was exchanged with row 2
- row 2 was exchanged with row 2
- row 3 was exchanged with row 3
We can satisfy ourselves that all is well, by factorising this permuted matrix:
- [math]\displaystyle{ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & \frac{1}{2} & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 \\ \frac{1}{3} & 1 & 0 \\ \frac{2}{3} & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 5 & 6 \\ 0 & \frac{4}{3} & -4 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 3 & 5 & 6 \\ 1 & 3 & -2 \\ 2 & 4 & 3 \end{bmatrix} }[/math]
Back to the theory page for a spell.
Solving Parabolic Problems using LAPACK
In our second example, we'll see 3 different schemes for solving a parabolic problem--forward Euler, backward Euler and Crank-Nicolson. The forward Euler scheme is explicit and so no system of linear equations is solved. It is a appealingly simple scheme, but can suffer from unstable solutions under certain conditions. In both the backward Euler and Crank-Nicolson schemes, we will see the (repeated) use of a pre-computed LU decomposition when solving a parabolic equation.
cd ../example2
In simple-crank-nicolson.f90 we see that the initial call to dgesv replaces the entries in the matrix A with an encoding of the LU decompostion (the unit diagonal is assumed). For subsequent timesteps we can thus call dgetrs instead:
do ii=2,4
...
call dgetrs('N', N, NRHS, A, LDA, IPIV, B, LDB, INFO)
...
end do
where we have remembered to take account of the boundary conditions at each time-step too:
do ii=2,4
...
! copy B into B1, so that we can recompute for
! the boundary conditions again.
B1 = B
! Need to recalculate entries for the vector of known
! values--held in B--given the solution at the current
! timestep--held in B1.
! *NB* the loops below are only valid for the case r=1.
! LHS
B(1,1) = 0 + B1(2,1)
! RHS
B(N,1) = 0 + B1(N-1,1)
! middle bit
do jj=2,N-1
B(jj,1) = B1(jj-1,1) + B1(jj+1,1)
end do
...
end do
Exercises
- Experiment with values of [math]\displaystyle{ r=\frac{k}{h^2} }[/math] for the 3 schemes, so as to highlight the effects of the CFL condition.
Banded Matrices
In all my examples, thus far, I've called routines from the dgexxx series offered by LAPACK. The d stands for double and the ge for generel purpose. For banded matrices, LAPACK offers a much more efficient format and routines to match. Take a look at http://www.netlib.org/lapack/double/ for a list of driver routines using matrices of double precision numbers, or http://www.netlib.org/lapack for more documentation in general.
PetSc: Iterative solutions and sparse matrices
In order to compute the solution of a linear system via the direct method of an LU-decomposition, we know that it will cost [math]\displaystyle{ O(n^3) }[/math] operations. Can we compute a solution more cheaply? The class of iterative methods strive to compute a cheaper solution by first guessing a value for the solution vector [math]\displaystyle{ x }[/math] and then iteratively refining it. Thus we will get a series of (hopefully!) improving approximations:
- [math]\displaystyle{ x^0, x^1, x^2, x^3, \cdots, x^j \rightarrow x }[/math]
By way of an illustration of such a method, consider splitting matrix A into 3 others:
- [math]\displaystyle{ A = L + D + U }[/math]
Note the summation, and so the L and the U matrices are not the same as those considered in the LU-decomposition used by the direct approach. With this split, Ax=b, becomes:
- [math]\displaystyle{ Lx + Dx + Ux = b }[/math]
The game now is to replace some occurrences of [math]\displaystyle{ x }[/math] by [math]\displaystyle{ x^k }[/math] and others by [math]\displaystyle{ x^{k+1} }[/math], and thereby obtaining a relationship which tells us how to get an approximation at one iteration step, from the approximation at the previous step. If the resulting iterative scheme converges, then we're in business!
One classic form of such an iteration is the Jacobi method (which is useful when A is diagonally dominant):
- [math]\displaystyle{ Lx^j + Dx^{j+1} + Ux^j = b }[/math]
- [math]\displaystyle{ x^{j+1} = D^{-1}(b - (L + U)x^j) }[/math]
To take a look at a illustrative implementation of the Jacobi method using LAPACK:
cd ../example3 make
and take a look at jacobi-example.f90. To run the executable, type:
./jacobi-example.exe
Happily, however, we do not need to write our own iterative schemes, as the good folk at Argonne have written the PETSc library.
http://www.mcs.anl.gov/petsc/petsc-as/
Take a look inside ex1f.F to see how to solve our laplacian example using PETSc. To run the program you will obviously need PETSc installed on the computer you are using. If you have, then edit Makefile and set PETSC_DIR to the appropriate value, and then type:
make ex1f qsub mpi_submit
Look in the file called OUT for the results of running PETSc.
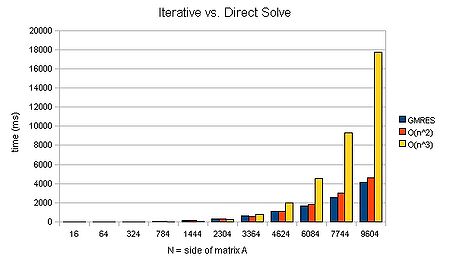
We can again plot a graph of timings given varying N:
We can see that an iterative method can scale approximately [math]\displaystyle{ O(n^2) }[/math]. For large matrices, this can mean that a solution is found several orders of magnitude faster. Now that is a speed-up worth having! It's liking buying a supercomputer than runs several orders of magnitude faster than your old one..
Better yet, you can try different schemes for iterative solution, just by varying some command-line arguments. For example:
./ex1f -ksp_type bcgs -pc_type jacobi
will invoke the biconjugate gradient stabalised scheme together with a jacobi preconditioner matrix. (This in fact runs faster than the GMRES method for the above case--808ms for N=9694. Note, however, that it cannot scale better than [math]\displaystyle{ O(N^2) }[/math].) For those interested, the PETSc manual is the best next port of call for more details on the various methods made available by the package.
For further examples see INSTALL_DIR/petsc-3.1-p1/src/ksp/ksp/examples/tutorials.
PLASMA: For Multicore Architectures
http://icl.cs.utk.edu/plasma/index.html
cd ../example4 make ./mxm-laplace-plasma.exe
For further examples, see e.g. INSTALL_DIR/plasma-installer_2.3.1/build/plasma_2.3.1.